I’ve been thinking about sharing interactive examples of some agent-based models for a while. And I had always thought of putting the code behind a running Python kernel that would then communicate with the front-end. But while learning Go, I came across an article about compiling Go code to WebAssembly, which can then be run natively on the browser.
In this post, I’ll show how I have created a simple interactive Schelling’s Model that runs entirely on the browser. The plan is then as follows:
- Implement Schelling’s Model in Go.
- Compile the code into WebAssembly.
- Integrate with HTML/JS to visualise the model.
Schelling’s Model
Schelling’s model, developed by economist Thomas Schelling, is an agent-based model of segregation in society. It demonstrates that even low levels of preference for similar agents can result in a segregated society.
The basics of this model I’ll implement (with some differences from the original model) are:
- There are two types of agents: orange and green.
- All agents are located in a unit square (\(0 <= x, y <= 1\)).
- An agent is happy if at least \(k/n\) neighbours are of the same type. Neighbours are the \(n\) agents closest to the agent in terms of euclidean distance.
- An unhappy agent moves to a location where they’d be happy.
Let’s initialise a Go project and call it schelling.
mkdir schelling
go mod init schelling
vim schelling.goWe’ll represent the model as a collection of locations and agent types.
type status struct {
xs, ys []float64
ts []bool
}Initialisation
During initialisation, we’ll randomly assign locations and type to agents.
// create agents and assign them location and type
locs := make([][]float64, 2)
locs[0], locs[1] = make([]float64, agents), make([]float64, agents)
ts := make([]bool, agents)
for i := 0; i < agents; i++ {
locs[0][i], locs[1][i] = rand.Float64(), rand.Float64()
ts[i] = rand.IntN(2) == 1
}
// run simulation
// ...Agent Happiness
To determine if an agent is happy, we need to identify the \(n\) closest agents to it, and then check if at least \(k\) of them are of the same type.
First let’s define a struct to record the distance to each agent and their type. Then we’ll also define a function to calculate the euclidean distance between two agents.
// Storing the distance and type of neighbours together so that when
// sorting neighbours by distance, we also keep track of their type
type neighbour struct {
d float64
t bool
}
// Calculate the euclidean distance between two points [x, y]
func distance(a, b [2]float64) float64 {
x := (a[0] - b[0]) * (a[0] - b[0])
y := (a[1] - b[1]) * (a[1] - b[1])
return math.Sqrt(x + y)
}Now let’s implement the code for checking if an agent is happy. When unhappy agents are considering moving to another location, they need to check if they’ll be happy at that location.
// Determine if agent at `idx` is happy at the specific `loc` location.
// The agent is happy if at least `k` out of `n` of its neighbours are
// of the same type `t`.
// Neighbours are the 10 closest agents based on euclidean distance.
// The locations and types of other agents are in `all`.
func isAgentHappyAtLocation(all *status, idx int, loc [2]float64, t bool, n, k int) bool {
var ns []neighbour
for i := 0; i < len(all.ts); i++ {
if idx == i {
continue
}
o := [2]float64{all.xs[i], all.ys[i]} // other agent
ns = append(ns, neighbour{d: distance(loc, o), t: all.ts[i]})
}
// now sort by distance and get the `n` neighbours
sort.Slice(ns, func(i, j int) bool {
return ns[i].d < ns[j].d
})
// check how many neighbours are of the same type
st := 0 // total neighbours of same type
for _, o := range ns[:n] {
if o.t == t {
st++
}
}
// is happy if number of same type agents > `k`
return st >= k
}
// Determine if agent at `idx` is happy within the status `all`.
func isAgentHappy(all *status, idx, n, k int) bool {
a := [2]float64{all.xs[idx], all.ys[idx]} // the agent
return isAgentHappyAtLocation(all, idx, a, all.ts[idx], n, k)
}
func unhappyAgents(all *status, n, k int) []int {
na := len(all.ts)
// get the happiness status for all agents
unhappy := make(chan int, na)
var wg sync.WaitGroup
for j := 0; j < na; j++ {
wg.Add(1)
go func(idx int) {
defer wg.Done()
if !isAgentHappy(all, idx, n, k) {
unhappy <- idx
}
}(j)
}
wg.Wait()
close(unhappy)
// copy channel into a slice and return
var indices []int
for i := range unhappy {
indices = append(indices, i)
}
return indices
}Moving Agents
When agents are unhappy, they move to a location where they will be happy, i.e., where at least \(k\) other agents are of the same type among the \(n\) neighbours.
The code runs in parallel for all agents - this means all agents are making decisions at the same time, and they can’t see what decisions others are making. So an agent might move to a location thinking it’ll be happy there, but concurrently other ‘same type’ agents might have moved from there, which means the agent will actually be unhappy there.
// `all` is the current status of all agents, and `unhappy` contains
// the indices of unhappy agents.
func moveAgents(all *status, unhappy []int, n, k int) {
var wg sync.WaitGroup
newLocs := make(chan [2]float64, len(unhappy))
for _, j := range unhappy {
wg.Add(1)
// keep looking until happy with new location
t := all.ts[j]
go func(idx int) {
defer wg.Done()
for {
// move to a new random location
newLoc := [2]float64{rand.Float64(), rand.Float64()}
if isAgentHappyAtLocation(all, idx, newLoc, t, n, k) {
newLocs <- newLoc
break
}
}
}(j)
}
wg.Wait()
close(newLocs)
// now update locations for all agents that moved
k := 0
for j := range newLocs {
idx := unhappy[k]
all.xs[idx], all.ys[idx] = j[0], j[1]
k++
}
}Testing the Simulation
Putting all the parts together, we can now run the simulation.
func main() {
// simulation parameters
agents, neighbours, sameType, iterations := 1000, 10, 5, 10
// create agents and assign them location and type
locs := make([][]float64, 2)
locs[0], locs[1] = make([]float64, agents), make([]float64, agents)
ts := make([]bool, agents)
for i := 0; i < agents; i++ {
locs[0][i], locs[1][i] = rand.Float64(), rand.Float64()
ts[i] = rand.IntN(2) == 1
}
// save initial state
allStatus = append(allStatus, &status{xs: locs[0], ys: locs[1], ts: ts})
// simulate
for i := 0; i < iterations; i++ {
cur := allStatus[i].deepCopy()
// indentify agents that aren't happy with their current location
unhappy := unhappyAgents(cur, neighbours, sameType)
if len(unhappy) == 0 { // stop if all happy
break
}
// allow unhappy agents to move until they've found a location where
// they will be happy
moveAgents(cur, unhappy, neighbours, sameType)
// update status
allStatus = append(allStatus, cur)
}
return allStatus
}Compiling to WebAssembly
The next step is to compile the model to WebAssembly. We want to be able to call the model from Javascript to run the simulations. This in turn requires passing data between Javascript and Go/WebAssembly, which will take place in the JSON format.
Therefore, we’ll need to add some glue code to our model to enable this communication. Go provides the syscall/js library for this purpose.
import (
...
"syscall/js"
)
// Convert status to Json
func (s *status) json() []any {
res := []any{}
for i := 0; i < len(s.ts); i++ {
res = append(res, []any{s.xs[i], s.ys[i], s.ts[i]})
}
return res
}
func jsonWrapper() js.Func {
jsonFunc := js.FuncOf(func(this js.Value, args []js.Value) any {
// 1.
if len(args) != 4 {
return "Invalid no of arguments passed"
}
agents := args[0].Int()
neighbours := args[1].Int()
sameType := args[2].Int()
runs := args[3].Int()
// 2.
status := Simulate(agents, neighbours, sameType, runs)
// 3.
json := []any{}
for _, s := range status {
json = append(json, s.json())
}
return json
})
return jsonFunc
}In the above code at (1) we’re converting JSON input into Go types, at (2) we’re running the simulation, and at (3) we’re converting the simulation results back into JSON for sending to the Javascript code.
Now we’re ready to compile to WebAssembly. We need to specify the OS and the architecture while compiling.
GOOS=js GOARCH=wasm go build -o schelling.wasmLinking with HTML/JS
The next step is to import the schelling.wasm file in Javascript and call the schelling model from there.
We first need to copy some additional JS glue code to use with the schelling.wasm file.
cp "$(go env GOROOT)/misc/wasm/wasm_exec.js" ./Lets start with a simple schelling.html file.
<html>
<head>
<meta charset="utf-8"/>
<script src="wasm_exec.js"></script>
<script src="https://cdn.jsdelivr.net/npm/d3@7"></script>
<script src="https://cdn.jsdelivr.net/npm/@observablehq/plot@0.6"></script>
<script type="text/javascript" src="schelling.js"></script>
<style>
datalist {
display: flex;
flex-direction: row;
justify-content: space-between;
writing-mode: horizontal-tb;
width: 200px;
}
option {
padding: 0;
}
input[type="range"] {
width: 200px;
margin: 0;
}
</style>
</head>
<body>
<div id="params">
</p>
<label for="happy_ratio">Neighbours of same type required to be happy:</label><br />
<input type="range" id="happy_ratio" name="happy_ratio" list="ratios" min=3 max=7 />
<datalist id="ratios">
<option value="3" label="3"></option>
<option value="4" label="4"></option>
<option value="5" label="5"></option>
<option value="5" label="6"></option>
<option value="7" label="7"></option>
</datalist>
<button onClick="run_and_visualise_simulation()">Simulate</button>
</div>
<div id="myplot">
</div>
</body>
</html>In the schelling.js file, lets import the schelling.wasm file.
const go = new Go();
WebAssembly.instantiateStreaming(fetch("schelling.wasm"), go.importObject).then((result) => {
go.run(result.instance);
});Then we’ll use the observable plot library to visualise the results. We need to transform the data into a format observable understands.
function data_for_observable(res) {
data = [];
res.forEach(function(iter, idx) {
iter.forEach(function(a, _) {
data.push({
x: a[0], y: a[1], type: a[2], iteration: idx
})
})
})
return data;
}Now we’ll produce some plots.
function observable_plot(data) {
dim = 200;
const plot = Plot.plot((() => {
const n = 3; // number of columns
const keys = Array.from(d3.union(data.map((d) =>
d.iteration)));
const index = new Map(keys.map((key, i) => [key, i]));
const fx = (key) => index.get(key) % n;
const fy = (key) => Math.floor(index.get(key) / n);
return {
height: dim * keys.length / n,
width: dim * n,
axis: null,
grid: false,
color: {type: 'categorical'},
inset: 5,
marginTop: 15,
fx: {padding: 0.1},
fy: {padding: 0.15},
title: "Simulation of Schelling's Model",
marks: [
Plot.dot(data, {
x: 'x', y: 'y', stroke: 'type', symbol: 'type',
fx: (d) => fx(d.iteration),
fy: (d) => fy(d.iteration),
r: 3,
}),
Plot.text(keys, {fx, fy, frameAnchor: "top-left", dx: 5, dy: -14, text: (d) => `iteration ${d}`, fontSize: 14}),
Plot.frame(),
]
};
})())
return plot;
}
function observable_facet_plot(res) {
data = data_for_observable(res);
plot = observable_plot(data);
const div = document.querySelector("#myplot");
div.append(plot);
}
async function run_simulation(na, nn, ns, nr) {
return await simulate(na, nn, ns, nr);
}
function run_and_visualise_simulation() {
na = 1000;
nn = 10;
ns = parseInt(document.getElementById('happy_ratio').value);
nr = 10;
res = simulate(na, nn, ns, nr);
observable_facet_plot(res);
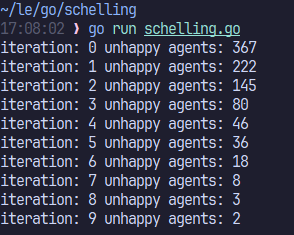
}And now this is what everything looks like. If you click on the Simulate button, it should load run the simulation and show you the visualisation.
Animated Visualisation with Plotly
With some more work, I was able to generate an animated visualisation of the agents move around the unit square with Plotly.